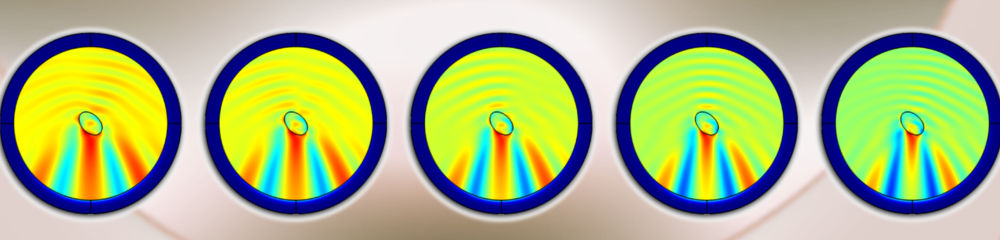
A new integro-PDE was proposed for a class of light transport problems involving bulk scattering media. The class of light transport problems modellable using our technique includes natural phenomena such as atmospheric, stellar or inter-stellar radiative transfer, as well as industrial phenomena such as light guides or light conducting materials having bulk scattering properties.
The integro-PDE features five dimensions, three in differential and two in integral form. The integral form can be imagined to be a “spherical integration” — i.e. a linear shift invariant system where “shift” is defined using the symmetry group of a sphere. (The dimensions go up to twenty if using partially polarized (Stokes / Mueller) calculus rather than photometric quantities.) Unfortunately, the symmetry of a sphere does not lend itself well to a good quantization scheme; consequentially, coding the solver involved very careful manipulation of spherical trigonometric quantities.
The final solver quantizes the direction dimensions, but does not quantize the spatial dimensions. Two of the spatial dimensions are “folded” using known or approximated spatial symmetry of the problem. The final spatial dimension is handled in partial closed form: we were able to derive the parametrized formula in closed-form for an eigenmode in this dimension, but the parameters in the formula are evaluated by solving a large eigenvalue problem involving all the dimensions.
Further optimization is achieved using known directional symmetries of the problem. Furthermore, the spherical (direction) domain is truncated — some of the directions are known to have negligible solution strength. This “sparsity pattern” is encoded into the formulation (rather than using ready-made sparse matrix techniques).
All this gives a solution to the integro-PDE, and that too in algebraic form (albeit with calculated constants). This solution is used to optimize features of the Mie scattering material, such as composition and concentration for achieving particular target optical effects. Interestingly, the concentration optimization problem leads to a new type of differential equation, leading to the unique situation where an ODE solver rather than a minimizer is used for an optimization problem.
Expertise
This project showcases the following expertise of Noumenon Multiphysics: